kNN

k-Nearest Neighbor Tutorial
1- Overview
kNN is a versatile Machine Learning algorithm that is based on a very simple principle, similarity of neighbors.
kNN is a non-parametric algorithm. No assumptions are made based on training data to reach predictions. This is likely one of the reasons why kNN performs surprisingly well in terms of accuracy.
Basically, kNN algorithms take a look at an assigned number of neighbors (say 5), and then make predictions based on comparison with those neighbors.
To sum it up, benefits of kNN are:
- It’s super intuitive and easy to grasp.
- It can do both Classification and Regression
- It’s impressively accurate even compared to most fundamental or sometimes complicated machine learning algorithms.
Distance parameter in kNN algorithm can be calculated using multiple methods:
- Euclidean Distance (p=2)
- Manhattan Distance (p=1)
- Minkowski Distances with arbitrary p value
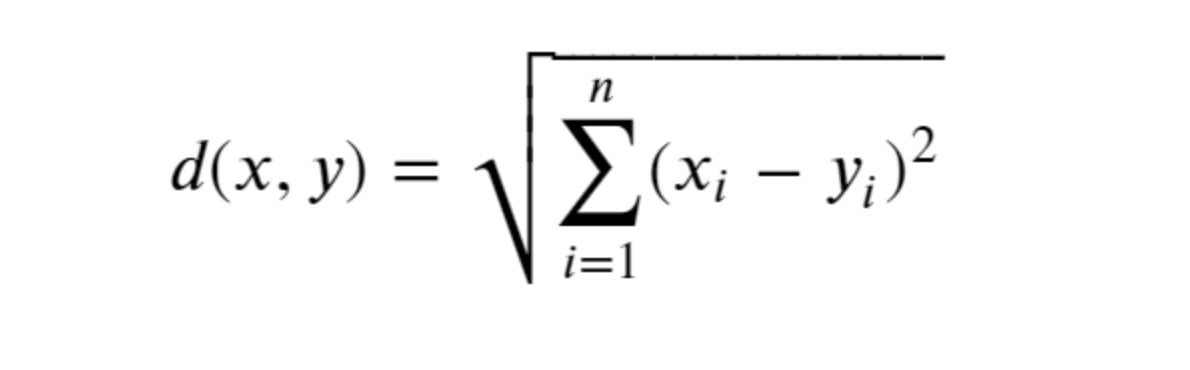
Why kNN Algorithm?
2- Benefits
kNN is a very intuitive machine learning algorithm that produces surprisingly accurate prediction results.
It works incredibly well out of the box. All you have to do is pretty much assign an optimum k neighbor value which is in many cases somewhere between 3-10. But don’t worry even that comes with a default value of 5.
Some of the more complicated parameters such as data search algorithm is also assigned to auto option which automatically finds the right algorithm based on training data.
kNN is our recommended machine learning algorithm for someone who is just starting to implement Machine Learning algorithms especially without a strong technical background.
But simplicity unfortunately comes with some cons. kNN may be inconvenient to scale or work with large data especially when many features are involved (high dimensionality). But you should check out the section below (Complexity and Performance) for more detail as there is lots of leeway to make kNN work even with very large datasets under some conditions.
kNN Cons
- Slow
- Scaling issues
- No probabilistic reports
How to Use kNN?
3- Building kNN Models
kNN works surprisingly well for both classification and regression problems. It can be applied using Scikit-Learn with very little Machine Learning and Python programming language experience. If you are impatient or just need a Machine Learning algorithm for some of your analytical tasks it can be the perfect Machine Learning solution that works well without the bells and whistles.
To build kNN models using Scikit-learn library just use the Python classes below:
(First you will need to import KNeighborsClassifier from sklearn.neighbors)
<code>from sklearn.neighbors import KNeighborsClassifier</code>
kNN Classification
- KNeighborsClassifier is a class that can be used for k-Nearest Neighbor Classification using Scikit-learn and Python.
SVM Regression
- KNeighborsRegressor: can be used to create k-Nearest Neighbor Regressor to work on regression problems using kNN in Scikit-learn.
You can find more details about kNN regression models in our article:
k is the main parameter that’s important to get right in kNN algorithm applications. There are also a few other parameters and settings that you may benefit from if more optimization is needed.
Recommended Reading:
Application Areas
4- Key Industries
kNN is commonly used in the industry for its intuitive and simple implementation and superb accuracy.
- Finance
- Medicine
- Cyber Security
- Retail
- E-commerce
Since kNN is good at both regression and classification, it’s probably better to ask: which specific fields kNN be used in and what are some of the specific examples to the solutions kNN solves?
- Computer Vision
- Clustering
- Outlier Detection
- Recommendation Engines
More specifically, below are some examples to the specific solutions kNN is implemented to solve:
- law (semantic search) similar documents court cases, rulings, defence documents, evidence, etc.
- online entertainment (recommender systems)
- ecommerce (recommender systems) books films electronics
- cybersecurity
- computer vision (face recognition)
- education – learning
Who Found kNN?
5- kNN History
kNN was found by two Berkeley statisticians during their consultation work for the USAF – United States Air Forces in 1951.
You can read more about kNN history in the article below:
Is kNN Fast?
6- kNN Complexity
Honestly, kNN is not the most performant Machine Learning algorithm but there are many cases it can still be fast enough and very useful. So, if you have a large data-set or you’re working on big data you may want to discover the dynamics that affect the different working aspects of the kNN algorithm.
The way kNN works is it calculates distance between neighbors, everyime a prediction is being made. When you think about this calculation it’s not very lightweight especially when done for each row and its features.
Another important point is that kNN does all the job on the go. During prediction all the calculations take place and training is merely about taking the data into the RAM. This means for prediction of each point kNN does the whole job from the start. Understanding this is important because kNN performance is so much about size of the data being predicted.
These calculations that take place during prediction are not necessarily light. Depending on the distance calculation method, it can be something like: 100 subtraction, 100 squares and 1 square root (Euclidean Distance) for every single row and for each feature.
Obviously, this will take lots of computation. Especially when the data set dimensionally grows (lots of features), we can end up with a sluggish algorithm that takes forever to predict. So, imagine a dataset with 10 million rows. Let’s say we split it 80/20 for training and test groups relatively. That makes 8 million training samples and 2 million prediction samples.
This means each time a point is being predicted in the data, kNN makes distance calculations for all of the sample size and applies it to the new point that’s being predicted and then repeats this for each prediction. This is because previous prediction will affect the neighbor relation of the upcoming prediction.
Runtime Test Summary
We have done some kNN speed tests for you. You can see more details regarding kNN runtime performance in the article below:
SINGLE PREDICTION
- 2 features
- knn – 2 features (1M rows) : 0.2250 secs
- 56 features
- knn – 56 features (1M rows) : 7.75240 secs
BATCH PREDICTION (Data as big as training sample size is being predicted at each step 50K, 100K, 200K, 1M relatively)
- 2 features
- kNN – 2 features (50K rows) : 1.2006 seconds
- kNN – 2 features (100K rows) : 2.4410 seconds
- kNN – 2 features (1M rows) : 6.9386 seconds
- 56 features
- kNN – 56 features (50K rows) : ~80 seconds
- kNN – 56 features (100K rows) : ~280 seconds
- kNN – 56 features (1M rows) : ~1015 seconds
Although our experiment was not done in sensitive lab environment it shows the shortcomings of kNN algorithm very well regarding scaling and time complexity.
We see that kNN starts to become quite problematic through the end of the experiment where feature size, data size and prediction size are all quite big for kNN algorithm. For example it took kNN algorithm to handle 1M predictions based on 1M data points with 56 features a staggering 17 minutes. Depending on the application this can be a very troubling performance or very tolerable performance.
kNN seems quite usable when single predictions are being made and/or if rows/features are relatively small. (up to 1M row is quite manageable with 2 features only at ~7 seconds). Otherwise some sort of dimension reduction or feature engineering will probably be necessary.
And if you have very few features and need prediction on very few data points kNN will still thrive as our little test turned in 2 features with 1M on single prediction in 0.2250 seconds only.
You can read more about kNN’s performance in the article below:
How can I improve kNN?
7- k-Nearest Neighbors Optimization
- n_neighbors: defines neighbor amount to be searched
- weights: defines weights of neighbors based on their distance
- radius: defines neighbors to be searched in specific radius value (if radius neighbor model is being used. See: kNN Classification).
Is there a kNN Implementation Example?
8- k-Nearest Neighbors Example
Here are examples that might be useful to understand kNN algorithm better.
kNN is a unique ML algorithm
kNN Questions Answered
- Why is kNN so impressive?
- Most impressive side of kNN algorithm is how accurately it can make regression and classification predictions. It doesn’t need much tuning either and its n_neighbors parameters is the most significant parameter that can be optimized.
- Why does kNN train faster than it predicts?
- Technically there is no training in traditional sense with kNN. It takes all the data to memory as far as training goes and all the calculations will be done at once during prediction phase. This makes training a mere data reading procedure while prediction phase of kNN is a whole lot of computation each time a point is being predicted.
- Also, since distance calculation is carried out for each row and for as many independent variables as there are, this step is computationally inefficient and requires lots of computing resources.
- Which kNN core algorithm is the best?
- It depends. brute tends to be more accurate but its performance can be pretty sluggish and ball_tree and kd_tree work well with large datasets.
How Do kNN Distance Calculation Methods Compare?
Euclidean vs Minkowski vs Manhattan
We have many distance calculation methods in scikit-learn intended to be used with kNN. For distance between vectors on the same dimensional space (such as two points on paper) following options are available and for 2 dimensional vectors (such as two points on Earth surface, since Earth surface has a curve) there is also Haversine distance calculation embedded in.
- Euclidean
- Minkowski
- Chebyshev
- Manhattan
- Wminkowski
- Seuclidean
- Mahalanobis
- Haversine
In scikit-learn these distance calculations can be assigned using “metric” parameter when constructing a kNN model. By default metric=”minkowski” and p=2. Please note that p=2 in minkowski distance calculation is equal to euclidean distance calculation and p=1 is equal to Manhattan distance calculation. Here is a practical example from scikit-learn:
knn=KNeighborsRegressor(n_neighbors=10, metric="minkowski", p=2)
kNN Regressor Model is created and assigned to variable knn using following parameters:
- k=10
- distance metric=minkowski
- p=2